Крачещи роботи чрез съчетано движение на тяло и крак

Веселин Павлов*, Иван Чавдаров**, Александър Вацкичев***, Валентин Николов *

*Технически университет, София, 1156, секция Роботика

**ЦЛМП-БАН, София, 1113, ул. “Акад. Г. Бончев”, бл.1

*** ИМБ-БАН, София, ул. “Акад. Г. Бончев”, бл.4

E-mails: vpavlov@hotmail.com, ivan_chavdarov@dir.bg, alex@imech.imbm.bas.bg, val_niko@yahoo.com.

Ключови думи: крачещи роботи, променлива геометрия, структури, походки, управление, програмиране.

Резюме:

Принципните решения за изграждане на крачещи роботи са много и в повечето случаи са изградени по аналогия на краченето в живата природа. В стремежа да се постигне висока мобилност и устойчивост на движение в неопределена среда се предлагат различни схемни изпълнения на краката и тялото. Обект на настоящето изследване е движението на четирикрака система с променлива геометрия и активни степени на свобода в тялото, с помощта, на които при последователно повдигане на краката се реализира специфична походка. Представена е конструкция и изработен физически модел за експериментални изследвания, система за управление и програмен продукт за моделиране на движението с прости и сложни походки.

1. Въведение

Крачещите роботи са динамично развиващи се област от мобилната роботика [7]. Тяхното най-съществено предимство е възможността за движение в труднопроходима среда с недетерминирани препятствия [6]. За преодоляване на препятствията и за запазване устойчивостта на робота е необходима висока мобилност, както по отношение на краката, така и на тялото. Крачещите роботи в по-голямата си част имат неподвижни тела (не променят формата си при движение), към което са закрепени определен брой крака, осигуряващи пълноценно преместване на робота в пространството. Неподвижното тяло създава определени удобства при проектиране, тъй като към него удобно се разполагат енергоносители, управляващите и сензорните устройства за.

Преодоляването на препятствия с по-големи размери, реализиране на завой с малък радиус, като и проблеми за по добра статична и динамична устойчивост биха се решили при подвижно тяло, в смисъл, тяло което променя геометричната си форма при движение [1, 2, 6]. Така е при повечето живи същества, които имат повишена мобилност и устойчиво движение при динамично изменящи се ситуации.

В настоящата работа се принципа за движение на крачещи роботи чрез съчетано движение на тяло и крак, респективно крака. Показани са структурни схеми и е изработен опитен образец на едно от възможните решения с елементарно движение на краката - линейно повдигане и спускане. Към тези подвижни тела могат да се присъединят кинематично пълноценни крака с три и повече степени на свобода всеки. Така мобилните възможности на робота нарастват значително и се подобрява статичната и динамичната устойчивост. Принципа на движение е приложим при двукраки, четирикраки, шесткраки и n-крака роботи, като “n” е четно число. По-подробно изследван в настоящата работа е четирикрак робот.

2. Структурни схеми.

Идеята за крачене с тяло може да се илюстрира при вертикално повдигане и спускане на краката. За да се различават краката при начертаване от въртящите и плъзгащите кинематични двойци е прието означение правоъгълник със закръгления. Пълноценната осем звенна равнинно затворена структура, която осигурява равнинно преместване на повдигнат е представена на фиг.1 при линейни и ротационни двигатели и комбинация между тях. При поликонтурно изпълнение (фиг.1 г) активните двигатели се свеждат до три.

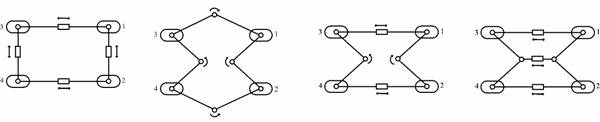
a) б) в) г)

Фиг.1. Структурни схеми на мобилни роботи с общо равнинно преместване (с две степени на свобода) на повдигнатия крак.

С въвеждането на ограничения в движението на повдигнатия крак и разположение на същия в шарнира, осемзвенната верига се свежда до шест звенна (фиг.2 а и б). Този подход за движение на краката е приложим и при двукраки роботи (фиг.2. в).

а) б) в)

Фиг.2. Схеми с два и четири крака

При шест крака (фиг.3) са необходими поне четири активни кинематични двойци (активните двойци са отбелязани със стрелки), при осем крака - шест и т.н. В основата на структурния синтез на този клас кинематични вериги (когато краката са разположени в шарнирите) стои активен шестзвенен затворен контур, който се свързва с всеки следващ с едно общо звено. Така при шест крака се получават единадесет подвижни звена, при осем крака - шестнадесет и т.н.

Фиг.3. Тяло с шест крака.

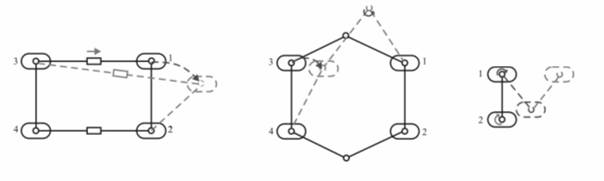
Съществува възможност да се намалят двигателите. Това се постига при отворена четиризвенна равнинна верига (фиг.4). Затварянето се постига чрез опорния крак, както е и при схемите на фиг. 2 а и б и фиг.3 . Тези схеми имат по-неблагоприятни предавателни функции при едни и същи метрични размери и при зададена товароносимост на робота изискват по-голяма мощност на двигателните устройства.

Фиг.4. Схеми с два и четири крака.

Движението при посочените схеми е с последователно повдигане на крак, при което в схемите с линейни активни двойци, преместването на четиризвенници. Изключение прави отворената схема с два крака.

Когато схемата е с шест, осем и повече крака, може да се повдига по един крак във всеки затворен контур без да се губи статична устойчивост. Вътрешните крака за общия контур могат да се повдигат последователно или едновременно. При тях кинематичните вериги са с две степени на свобода и трябва да се управляват съответният брой двигатели.

За да се запазва успоредната ориентация на краката могат да се използват паралелограмни механизми или техни аналози: зъбно-ремъчни или верижни предавки с предавателно отношение единица.

Възможните структурни схеми при избрания принцип на движение нарастват при комбинация на степента на затвореност на равнинната верига.

3. Модел за експериментални изследвания.

Общ изглед на робота е показан на фиг.5. Краката (1) и транслационните (2) модули реализират съответно вертикално и хоризонтално преместване, което се осъществява чрез постояннотоков електродвигател и винтов механизъм.

Повдигането на краката се осъществява посредством мотор-редуктор (1.1), свързан с винто-гаечна предавка (1.2) чрез съединител (1.5) . Опорната част на крака завършва със „стъпалото” (3). Стъпалото е конусна чашка, която контактува с периферната си част към пода и има пасивна ротация към винта. Четирите крака са еднакви. Направляваща (1.3) предпазва двигателя от завъртане. Височината на повдигане на крака се контролира с оптрони (1.4). В изпълнения модел се дефинира горно и долно крайно положение. Не представлява проблем поставянето на няколко оптрона и така чрез определена дискретна стойност да се управлява височината на повдигане на крака в определен диапазон. Това би оптимизирало движението и е интересно при прескачане на препятствия.

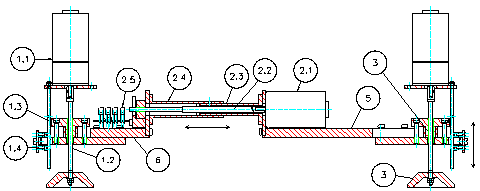
Фиг.5. Общ изглед на четирикрак робот с променлива геометрия на тялото

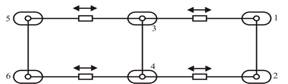
Тялото на робота е шест звена равнинна кинематична верига с четири пасивни шарнирни и две активни призматични двойци. Призматичните двойци (фиг.8) са реализирани по описаната по-горе схема – двигател, винто-гаечна предавка и система от оптрони.

Фиг.7. Механизъм за задвижване на крака.

Винтът (2.2) е свързан към ротора на двигателя (2.1). Към статора свързан със звено (5) е монтирана тръба (2.3), която обхваща винта (2.2) и влиза в тръба (2.4), неподвижно свързана със звено (6). Към звено (6) е монтирана неподвижно и гайка, в която се навива винта. Така при повдигнат крак свързан със звено (6) и управляван двигател (2.1) се реализира линейно движение в затворената равнинна верига, което премества крака в желаната посока (напред или назад). Преместването на крака съдържа и едно завъртане около неподвижна точка, радиуса на което зависи от дължината на звено (4). По този начин се постигат две независими степени на подвижност за всеки крак – повдигане и преместване. Стойността на линейното преместване се контролира, чрез последователно разположени оптрони (2.5), които се активират от преместването на винта. Чрез оптроните се управлява големината преместването на краката.

Пълният вид на робота заедно със електронните управляващи модули е представена на фиг. 9.

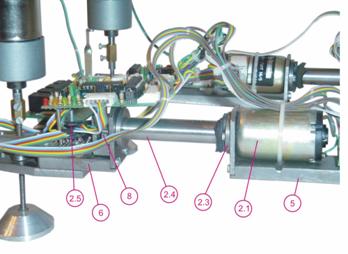
Фиг.8. Транслационни модули.

Фиг.9. Крачеш робот с променлива геометрия на тялото.

4. Генериране на походки и траектории.

Статична устойчивост на крачещи роботи, както е известно, може да се реализира при четири и повече крака. Съществена разлика между походките на роботи с неподвижно тяло и достатъчен брой степени на свобода на краката (минимум 3) и тези които се предлагат, няма [12]. Особеното е, че при последните конфигурацията на опорните точки съвпадат с тази на подвижното тялото. На фиг.10 са показани комбинациите при четири крака. Краката са отбелязани с числата 1, 2, 3 и 4. Принципните схеми на ходене при четири крака са две: 1234º2143 и 1324º2413 респективно1423º2314.

При четири крака движението с динамична устойчивост може да се реализира при повече схеми за последователно повдигане преместване и спускане на каката. Схемите позволяват повдигане на два крака диагонално разположени – едностранно.

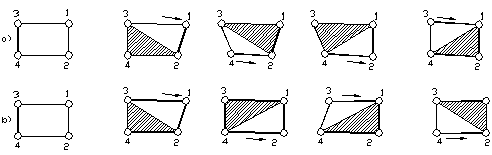
Фиг. 10. Походки при четири крака.

При схемите с диагонално свързване на задвижващите кинематични двойци (фиг.2) се реализират същите походки. Предлаганите схеми позволяват движение и с динамична устойчивост. В този случай трябва да има съчетано движение между повдигането, преместването и спускането на определен крак. Спускането може да се покрива с изправянето на “тялото”, така че люлеенето на масовия център да остава в допустимият интервал на преместване.

Както беше споменато преместването на робота от една позиция в друга се реализира с помощта на две активни призматични двойци, т.е. позиционната задача се решава при известни постоянни линейни размери на звената (L4, L5 и L6) на равнинната верига и стойността на обобщените координати: q = [h₁, h₂] ^T, където h1 и h₂ са линейни променливи.

Правата и обратната кинематични задачи, в случая могат да се решават аналитично (векторен метод, тригонометрични функции) и графично. При последното позицията на повдигнатия крак се определя чрез намиране пресечните точки на две окръжности (r1=l и r2= h_i + ∆h_i ). От възможните две пресечни точки се избира тази, която е в дефиниционната област на ставните ограничения.

При движение по права линия краката получават еднакво преместване, повдигнати последователно по един, в избран ред или два диагонално разположени. Схемата не позволява едновременното повдигане на двата крака управлявани от една активна призматична двойца, тъй като в този случай механизмът е с две степени на свобода.

Създаването на елементарна траектория преминава през три стъпки фиг.11.

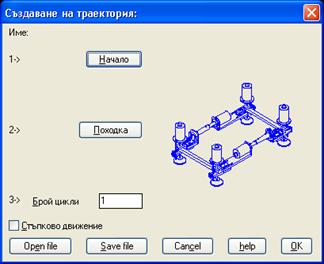
Фиг.11. Стъпки за създаване на елементарна траектория

НАЧАЛО - Понеже робота може да променя формата на тялото си, необходимо е да се зададе какво е началното и състояние. Възможни са конфигурации, при които формата е произволен четириъгълник (; h_{1_0} ¹ h2_{_0}), правоъгълник (; h_{1_0}=h_{2_0}), или успоредник (; h_{1_0} = h_{2_0}). Точните геометрични параметри се ограничават от ставните ограничения и хода на транслационните модули. Задава се и ориентацията на мобилния робот спрямо неподвижна координатна система (ъгъла a₀ ) фиг.12.

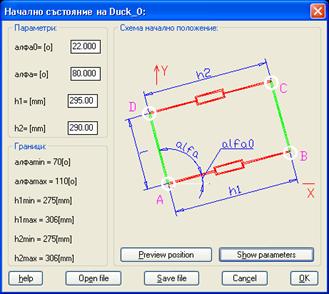
Фиг.12. Начално положение.

ПОХОДКИ - В програмата статичните походки са разделени на две: проста при която избрана последователност на преместване на четирите крака се повтаря многократно и сложна - произволна комбинация от n прости походки се повтаря многократно фиг.13.

Фиг.13. Видове походки. Фиг.14. Създаване на походка.

Последователността на преместване и хода на краката се задават в диалогов прозорец фиг.14. Моментното състояние на многокраките системи се описва с вектор на състоянието от вида: k = [k¹, k², .. kⁿ], където n е броя на краката, а kⁱ = 0 или 1, ако крака е опрян на земята или не [1]. Например k = [0,0,0,0] – означава, че всички крака са опорни. Походка се нарича последователността от състояния k_n , n = 1,2,…m. Походките могат да бъдат циклични или не. Цикъл c се нарича броя различни състояния, които се повтарят периодично.

Простата походка в конкретния случай е циклична с цикъл „c” = 8. Реализирането на сложна походка може да е циклично с c ³ 16 или не циклично движение. Матрицата G, описваща един цикъл при проста статична походка може да има вида :

Матриците G₁, G₂ и G₃ изразяват съответно – последователна походка, диагонална и тръст. L_i означава ляв, а R_i десен крак. Походката на N – крака манипулационна система е правилна когато G има 2N реда и N стълба. Цикличната замяна на редовете на свързаната (с походка) матрица G с правилна походка както и произволното разместване на стълбове довеждат до създаване на нови правилни походки. Походката G₃ е възможно да бъде статична (ако Dh_i е съобразено с радиуса на стъпалата, разпределението на масите и наклона на терена), или динамична. При нея c =4.

Информацията за последователността на повдигане на краката не е достатъчна за управление на движенията на системата, необходимо е за всяко състояние k_i да са дефинирани обобщените координати q_i за транслационните модули. Техните нараствания се задават в диалоговия прозорец фиг.14. В зависимост от избора на последователност на повдигане на краката и съответните им h_i+Dh_i , могат да се реализират различни походки и траектории фиг.15.

От начално положение успоредник или правоъгълник лесно се реализира траектория по права линия с помощта на проста походка фиг.15 а), b), c). Когато е необходимо да се промени ориентацията на МС или движение по дъга с проста походка, могат да се постигнат само ограничени движения, понеже се променя геометрията на МС и неизбежно се стига до ставно ограничение фиг.15 b), d), e).

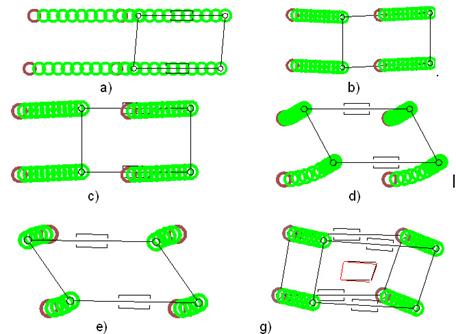
Фиг.15. Траектории, реализирани с проста походка.

Необходими са компенсиращи стъпки, които се постигат със сложна походка. Походките от фиг.15 a), b) и c) са вълнови – матрицата G се повтаря циклично, а всеки един от краката се премества на еднакво разстояние сравнено с останалите и компенсира предходно преместване на крак. Ако началното положение е правоъгълник при изпълнение на n цикъла с вълнова походка, манипулатора запазва първоначалната си геометрия фиг.15. a), b), c). Когато изходната геометрия е произволен четириъгълник прилагането на вълнова походка не запазва геометричната форма фиг.15.g). Важно значение има знака на нарастването Dh_i както и нарастването му. Възможни са комбинации при които периодично да се компенсират дължините h_i и такива при които въпреки ползването на циклична походка да се достигне до промяна в геометрията на механизма която не отговаря на ставните ограничения Фиг.15.

5. Модел на робота в среда на 4D Visual Nastran.

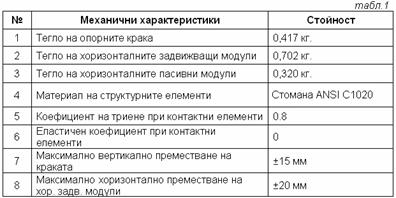
Устойчивост на крачещия робот е симулирана в среда на 4D Visual Nastran чрез компютърен модел [10], създаден в AutoDesk Inventor. При моделирането са използвани всички детайли на робота с реалните им размери и характеристики. Някои от механичните параметри на структурата са посочени в табл.1.

Възможностите на софтуерната среда позволяват да бъде анализирана както статичната, така и динамичната устойчивост на робота. Определят се всички активни и пасивни действащи сили върху звената му. Във връзка с това са избрани различни симулационни параметри – скорост и ускорение в активните двойци, точност на симулираните движения (позиционна, монтажна, степен на “проникване” при контактни обекти). Конкретните стойности на тези параметри са посочени в табл.2.

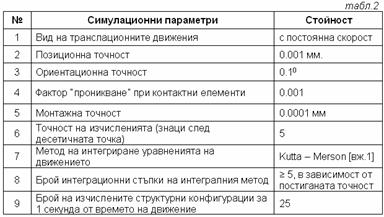
Трябва да бъдат отбелязани следните особености на симулационния процес:

- софтуерната среда определя редундантните ограничения, наложени от реалните двойци. При изчисляване на силите върху звената тези ограничения се нулират до свеждане на системата до статично определима.

- контактът между краката и пода е симулиран на базата на системата “пружина - демпфер” при лимитирано “проникване” между контактуващите тела. Характерен момент е изборът на пружинната константа и коефициента на затихване на вибрациите в краката при допир с пода. Пружинната константа е свързана с факторът “проникване” между контактните елементи (табл.2, поз.4). При увеличено проникване в рамките 0.1 – 0.01 е намалена вероятността от плъзване на даден крак по плоскостта на пода под действието на хоризонтални сили. Такова “проникване” обаче е свързано с увеличени еластични сили и избор на оптималното им демпфиране. В конкретният случай трите свързани параметри “проникване -пружинна константа - коефициент на демпфиране” са подбрани опитно, на базата на симулации и измерване на микро движенията на краката при контакт с пода. Като оптимални са определени тези коефициенти, при които вибрациите и приплъзването на краката при контакт не надхвърлят зададената позиционна точност (табл.1, поз.2).

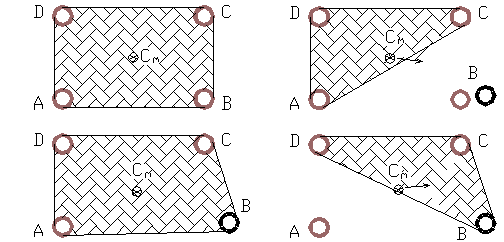
Фиг.16. Статична устойчивост

Създаденият компютърен модел е използван за анализ на статичната устойчивост на робота. Тя е гарантирана когато центърът на тежестта му С_m не излиза от многоъгълника, образуван от външните контури на опорните стъпала (фиг.16). При преодоляване на наклони е необходимо проекцията на центъра да остава в описания контур.

Устойчивостта на разглежданата манипулационна система е симулирана при две походки:

а) Симулация при последователно преместване на всеки крак – движението на краката е интерполация между вертикалното им преместване и движение напред на съответния хоризонтален модул (фиг.17).

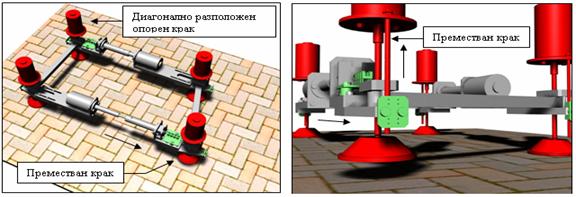
Фиг.17. Хоризонтално, вертикално и преместване на 1 крак при походка 4х1

Резултатите от симулацията на робот с реални тегла на елементите са представени на фиг.18.

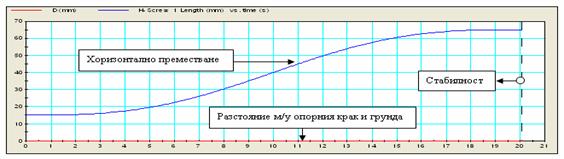
Фиг.18..Стабилност на 1 крак при реално тегло и тегло, увеличено с 50%.

По абсцисите на графиките е времето на движение t, а по ординатите преместването на хоризонталния модул напред и разстоянието между диагонално разположения опорен крак и терена. От графика 1 се вижда, роботът запазва стабилността си, т.е. диагоналния крак не се повдига и структурата не се накланя дори при тегло на премествания крак увеличено с 50% над реалното.

При симулацията, представена на фиг.19, теглото на премествания крак е увеличено със 100%.

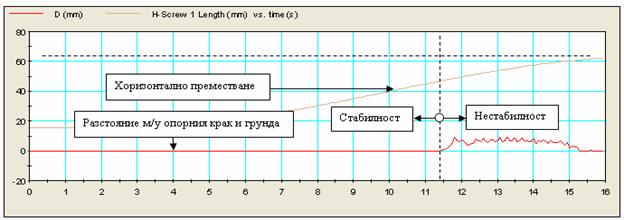
Фиг.19. Нестабилност на робота при тегло на премествания крак, увеличено със 100%.

Роботът губи стабилност и повдига диагоналния опорен крак при хоризонтално премесване на крака около 47 мм, което значително надхвърля реалните ограничения.

б) Симулация при едновременно преместване на диагонално разположените крака (фиг.20) Краката на робота се повдигат и преместват напред два по два. Скоростта на движение при тази походка е два пъти по-голяма от симулираната и описаната в подточка (а).

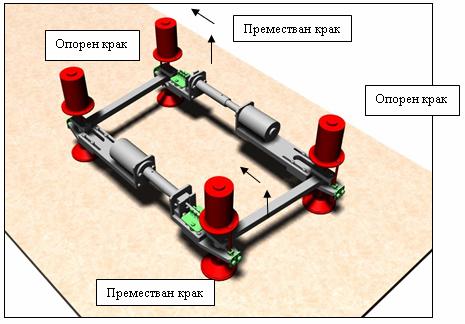
Фиг.20. Опорни и премествани крака при походка 2х2.

При реални тегла на елементите роботът запазва стабилността си благодарение на цилиндричните стъпала. В хода на симулацията е контролиран наклонът на диагоналните опорни стъпала. За пълния диапазон на

хоризонтално преместване на краката този наклон остава постоянен (вж.фиг.21), т.е. структурата не се накланя и не губи стабилност. Единственото движение е равнинна ротация на краката около вертикална ос (вж.фиг.21).

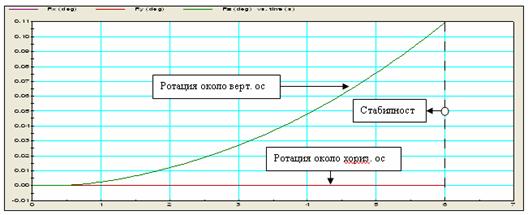
Фиг. 21. Стабилност при пълен диапазон на хоризонтално преместване на краката

6. Управление

Роботът не притежава собствен процесор, поради което организацията на работата му се поема от компютър. Представя се хардуера , протоколите и софтуерното осигуряване, благодарение, на които става възможно управлението на робота.

Управлението на робота, става през паралелният порт, посредством кабел. Независимо от положението си в адресируемата памет, всички паралелни портове използват един и същ регистров интерфейс, който се състои от три порта. Текущо се използват само два от тях – 8 битова „линия данни”, използвана за предаване на информация към робота и 5 битова „линия проверка на състоянието” за обратната връзка от оптичните сензори. Съществува директна връзка между битовете на портовите и жиците в паралелния кабел (фиг.22). Стандартът CENTRONIC описва съответствието, между изводите на всеки порт и линиите в кабела. Ако един бит в някой от регистрите е вдигнат, тогава по съответната жица се изпраща сигнал. Обратно, ако стойността му е нула, тогава не се изпраща сигнал. Текущото състояние на тока по жицата винаги отразява положението на съответния бит в регистъра на порта, който се управлява от софтуера.

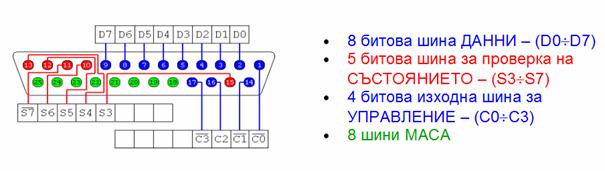
Фиг.22. Паралелен порт-изводи

От едната страна на кабела е монтиран стандартен куплунг CANON 25, за връзка със паралелният порт, а от другата IDC14DH, която се свързва към куплунг BH14R (фиг.23) монтиран върху робота.

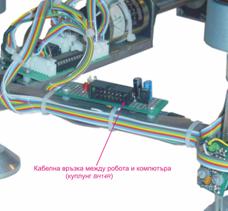
Фиг.23. Комуникационен конектор

В софтуера е заложено в даден момент от време да бъде управляван само един двигател, но не съществуват хардуерни ограничения да бъдат задвижвани едновременно и повече (при динамична устойчивост). От осемте възможни бита от изходния регистър, за управлението на робота се използват само шест. Бит D0 разрешава/забранява управлението на робота. Битове D1¸ D3 са адресиращи и се използват за избор на определен двигател, към който текущо е насочено управлението, а D4 и D5 определят посоката на въртенето му.

При разработката на хардуера е заложен модулният принцип. Използват се две основни модулни платки. Едната е т.н „селектор”, където в зависимост от логическата комбинация в адресиращите битове (D1¸ D3) се избира съответен двигател, който да бъде управляван. В същото време селектора следи и предава към компютъра информацията от сензорите, следящи положението на двигателя. В този момент управляващите и шините от обратните връзки към останалите електродвигателя са във високоимпедансно състояние. Принципната схема на селектора може да се види на фиг.24, а негова снимка на фиг.25.

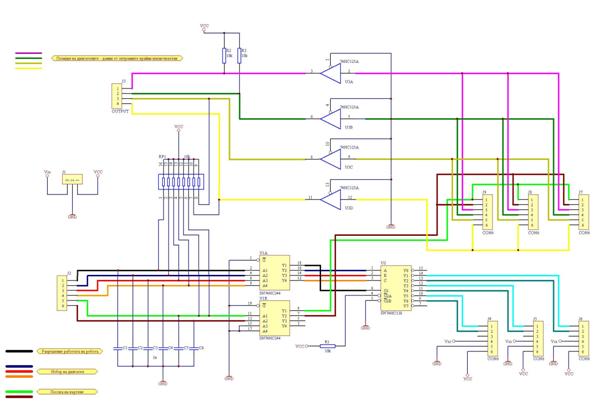
Фиг. 24. Селектор.

Фиг.25. Селектор

Вторият – „изпълнителен” модул съдържа драйверни схеми (H-мост) управляващи двигателите, както и буфери следящи сензорите от обратните връзки. С един такъв модул могат да се управляват два електродвигателя.

Връзката между комуникационния конектор (фиг.24) и входно/изходните изводи от селектора става посредством плосък кабел. Конектор J2 се явява входен за схемата. През него управляващите битове постъпват на входна буферна верига. Целта е да се подтиснат смущения предавани по комуникационния кабел. С помощта на резисторната матрица RP1 (10k) се повдига нивото на пристигащите и изпращаните логически сигнали, а чрез кондензаторите С1¸С6 се филтрират входни шумове. Ролята на буфер се изпълнява от U1 - 74НС244. Преминали през него първите четири бита от входната шина (U1 изходи 18, 16,14, 12) се подават към 8-битовият дешифратор 74НС138. Разрешаващият бит (D0 –извод18) се свързва, към вход G1₍₆₎. За нормалната работа на дешифратора, на входове G2A₍₄₎ и 2B₍₂₎, трябва да бъде подадена лог.0, а на G1 лог.1, в противен случай всички изходи получават високо логическо ниво независимо от състоянието на адресните входове А₍₁₎, В₍₂₎, С₍₃₎. Когато, чрез разрешаващият бит се изпрати лог.1, комбинация от адресните входове определят, кой от изходите (Y0¸Y7) да премине в лог.0. Именно това ниво активира схемите управляващи отделните двигатели. В даден момент само един изход може да има ниско ниво. От принципната схема се вижда, че с адресните комбинации 000 и 111 не се управляват двигатели, тъй като съответните изходи (Y0 и Y7) не се използват. Стана ясно, че всеки изпълнителен модул може да управлява по два двигателя, така че в конкретният случай за шестте двигателя се използват три такива модула. Посредством кабел към конектори J4¸J6 се свързват трите изпълнителни модула, като освен двете шини за избор на двигател се подават захранващите електрониката (V_CC) и двигателите (V_SS) напрежения.През буфер U3-74НС125, към компютъра се подава информацията от конектори J7¸J9, която отразява състоянието на сензорите към двигателя, който е управляван в момента. Към компютъра могат да бъдат изпращани максимум четири бита. Чрез тези конектори става подаването към изпълнителния модул на двата бита определящи посоката на въртене на двигателите (U1- Y1₍₉₎ и Y2₍₇₎).

Принципната схема на изпълнителният модул е представена на фиг.26.

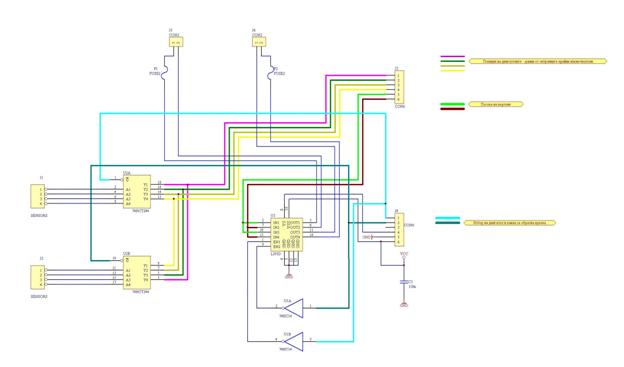
Фиг.26. Изпълнителен модул.

Известни са много схемни решения за управление на постояннотокови двигатели, всяка от която има своето предимство, което определя и специфичното и приложения. За управлението им в случая се използва Н-мост в интегрално изпълнение. Интегралната схема L293 (фиг.27) включва в себе си два Н-моста и позволява управлението на два електродвигателя, като максималният ток, който може да се осигури е 600 mА на канал.

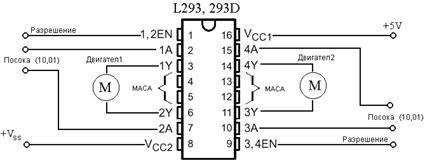
Фиг.27. L293 – два интегрални Н-моста в един корпус.

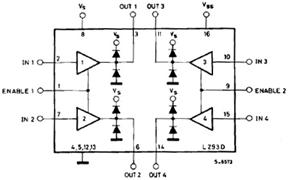
Фиг.28. L293D – блокова схема и таблица на истинност.

Предлагат се няколко разновидности на тази схема - L293, L293А, L293B, L293D. Схемите са със сходни параметри, но е използвана L293D, която е с вградени защитни диоди и не се налага добавянето им допълнително.

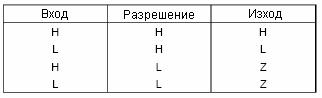
От таблицата на истинност представена на фиг.28 се вижда, че за да работи Н-моста, на входа му за разрешение трябва да бъде подадено високо логическо ниво. В противен случай изходите му преминават във високоинпедансно състояние. Друго условие за да се завърти двигателя в определена посока е на входовете му да се подадат противоположни логически нива – 10 или 01. На 16-ти крак на интегралните чипове се подава напрежение за логиката V_CC=5 V, а на 8-ми крак V_SS=12V за захранване на електродвигателите. На изходите, паралелно на двата двигателя се включват кондензатори със стойност 10 nF за филтриране на високочестотните шумове, генерирани от четковата система.

Фиг.28. Изпълнителен модул

От фиг.26 се вижда, че през конектор J4 двете активиращи шини постъпват на разрешаващите входове на L293D и тези на буфера U2-74НС244. Нека приемем, че към извод „1” на J4 от селектора пристигне лог.0. Тази нула постъпва на разрешаващия вход G₍₁₎ на първата секция от буфера U2. При това положение сензорната информация от вход J1 се предава към изходи Y1₍₁₈₎, Y2₍₁₆₎, Y3₍₁₄₎, Y4₍₁₂₎ и от там към конектор J3, която ги изпраща, към селектора. Изходите на втората секция от буфер U2 остават във високоимпедансно състояние, тъй като на разрешаващия му вход G₍₁₉₎ логическото ниво е високо. В същото време на разрешаващият вход ЕN1(1) на L293D постъпва високо ниво, тъй като лог. нула се инвертира от U1. Ако в този момент двата управляващи посоката битове (изводи „5” и „6” от J3 свързани към входовете на L293D) са противоположни двигателя свързан към конектор J5 ще се завърти. Другият двигател ще остане неподвижен, поради факта, че нивото на разрешаващият му вход EN2₍₉₎ е ниско, независимо от това, че на входовете му за посоката е подадена същата комбинация.

Като обратна връзка, отчитаща положението на електродвигателите, се използват оптронни двойки. Във всеки от кратката има по два оптрона отчитащи крайно горно, и крайно долно положение, т.е използват се само два бита от четирите възможни (фиг.26 – J1 и J2). За да бъде възможно отчитането, в направляващите пластини са прорязани отвори.

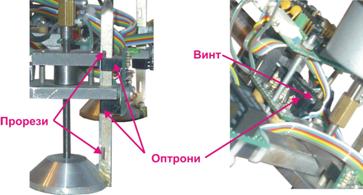
Фиг.29. Разположение на оптронните двойки.

При транслационните модули са монтирани по четири оптрона, с което може да се регулира големината на хоризонталното преместване. Прекъсването на светлинния поток в случая става от винта реализиращ транслацията На фиг.29 е представено разположението на оптронните двойки.

За да може да бъде по-достъпно управлението на робота, е разработен интерактивен софтуер върху Windows XP базирана платформа. Интерфейса на програмата е представен на следващата фигура.

Програмата има три режима на работа: Инициализация, Ръчно управление и Програмно управление.

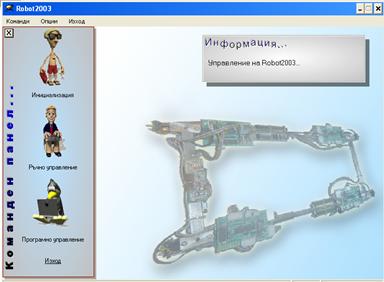
Фиг.30. Управляващ софтуер – главно меню.

- Инициализация: Използва се при първоначално включване на робота за автоматично повдигане на краката до максимално горно положение

Фиг.31. Инициализация.

- Ръчно управление: В този режим с помощта на клавиатурата оператора избира двигател, който да бъде управляван. След като е маркиран, управлението, нагоре/надолу - за краката или напред/назад – за транслациите, става посредством стрелките. Във всеки един момент информацията от сензорите се визуализира върху екрана. Предвидена е автоматична блокировка на движението и аларма в случай, че управлявания двигател достигне до крайно положение.

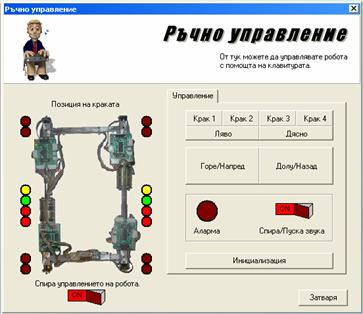
Фиг.32. Ръчно управление.

- Програмно управление: Има възможност за предварително записване на походки и програми за движение на робота.

7. Заключение.

Предлаганите схеми на мобилни роботи, крачещи чрез съчетано движение на тялото и подвижния крак, осигуряват пълноценно движение в равнина. Всеки подвижен крак получава две премествания, посоката и стойността на които се управлява целево. Подвижността в тялото е свързана с промяна на неговата геометрична форма, което благоприятства статична устойчивост и може да се използва при заобикаляне на препятствие. Движението по права линия се реализира със проста походка, а реализирането на завой предполага сложна походка.

Изградените реален и виртуален модел на избраната схема позволяват да се извършат по-прецизно изследване за определяне разпределението на масите върху подвижните звена на тялото с цел увеличаване на статичната устойчивост на робота при завой и преодоляване на препятствия.

В активните двойци на затворения контур се използват диференциалният ефект на винтов механизъм, което позволява чрез един активен двигател да се управлява преместването на два крака, които имат последователно действие при движението на робота.

Управлението на робота се извършва от компютър, което дава известна свобода при проектирането на управляващ софтуер. Използването на кабел като средство за комуникация освобождава робота от необходимостта да носи върху себе си допълнително микропроцесорно управление и електрозахранвания блок. Модулността в изграждането на електронния хардуер осигурява гъвкавост, особено при бъдещи модификации на механичната структура свързани с добавянето или премахването на двигатели.

8. Литература.

[1] Chen, I-M. and Yeo, S. H. 2002. Locomotion and navigation of a Planar Walker based on binary actuation. In Proc. IEEE International Conference on Robotics and Automation, Washington DC, USA, pp. 329-334.

[2] Chen, I-M. and Yeo, S. H. Locomotion of a Two-Dimensional Walking-Climbing Robot Using A Closed-Loop Mechanism: From Gait Generation to Navigation. The International Journal of Robotics Research Vol.22, No. 1, January 2003, pp. 21-40.

[3] Quinn, R. D., Nelson, G. M., Bachmann, R. J., and Kingsley, D. A., Allen, T. J. Parallel Complementary Strategies For Implementing Biological Principles Into Mobile Robots. The International Journal of Robotics Research Vol. 22, No. 3-April, March-April 2003, pp.169-186.

[4] Tanev T., Manipulation systems based on variable-geometry modules, Mechanic of machines, ISSN 0861-9727, Varna, 1996.

[5] Tartikainem К., Halme А. & Karkkainem K.. Terrain adaptive motion and free gait of a six-legged walking machine, 1^st, FAC Workshop on Intelligent Autonomous Vehicles. Southampton, UK, April 1993.

[6] Bretl, T., Latombe, J-C., and Rock S. Toward Autonomous Free-Climbing Robots.

[7] Klark D., Owing M., Building Robot Drive Trains, www.books.mcgraw-hill.com, 2003.

[8] Robot Information Central, www.robotics.con/robots

[9] Walking and climbing machines, www.fzi.de/ids/wmc/vedeos/videos

[10] Вацкичев Aл., Павлов В., Чавдаров И., Николов В., Изследване на статичната устойчивост на четирикрак мобилен робот с променлива геометрия на тялото, Научни известия на НТС по машиностроене, ISSN1310-3946, том 10, брой 5, октомври 2003, стр. 2.75- 3.0.

[11] Павлов В., Николов В., Чавдаров И., Мобилни роботи с “патешка” походка, Седма международна конференция Практро ’2003, Варна 10-14 юни, “Сборник доклади ПРАКТРО’2003”, стр. 272-277.

[12] Чавдаров И., Павлов В., Вацкичев Ал., Николов В., Моделиране движението на четирикрак робот с променлива геометрия на тялото, Научни известия на НТС по машиностроене, ISSN1310-3946, том 10, брой 5, октомври 2003, стр. 2.68-2.74.

[13] Охоцимский Д., Голубев Ю., Механика и управление движением автоматического шагающего аппарата, “Наука”, Москва, 1984.